Applying MATSim to Study Movement Across Campus: Steps and Takeaways
By Alex Raposo ’22
As a GRI Summer Fellow, Alex Raposo worked with Frank Qiu and Luca Paravano under the instruction of Data Science Professor Tyler Frazier to develop a model of student movement on the William & Mary campus. Read on for a Q&A to learn how the team went about this project and what long-term impacts this work could have on changes to infrastructure.
What did you enjoy most about working on this project?
The collaborative environment fostered within our team allowed me to actively learn while honing my problem solving skills. I also enjoyed exploring the applications of my existing knowledge and identifying areas of data science in which I could improve. I look forward to continuing this important research throughout the coming school year!
What tools did you use to create the model?
To implement an agent-based model, we used the Multi-Agent Simulation (MATSim) framework in Java. Models developed in MATSim are based on the “co-evolutionary principle,” so they are structured to reflect a constant competition for optimal daily travel under the space and time constraints of existing transportation infrastructure.
How did you track movement and account for daily variation?
Each agent represented in the model is associated with a travel diary that contains a fixed number of daily plans. Plans are collections of sequential activities representing an agent’s movement throughout a day. Although plans are defined by the user, MATSim also randomly generates some plans using a replanning module. Replanning allows us to account for unanticipated agent choices. Because plans are composed of activity coordinates, MATSim is also responsible for determining the routes and modes of transportation used to commute between these activities.
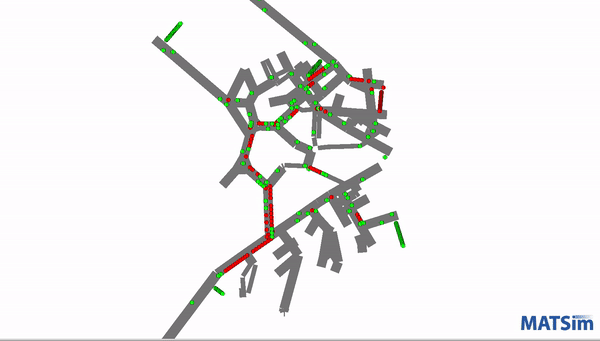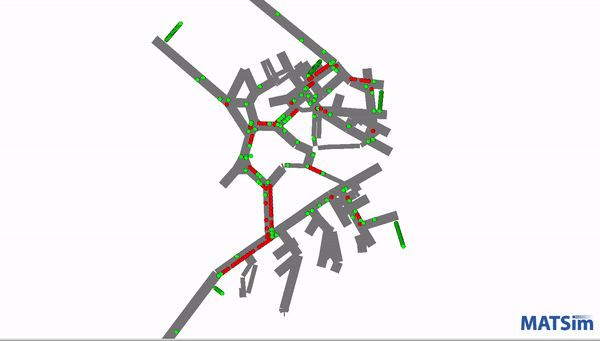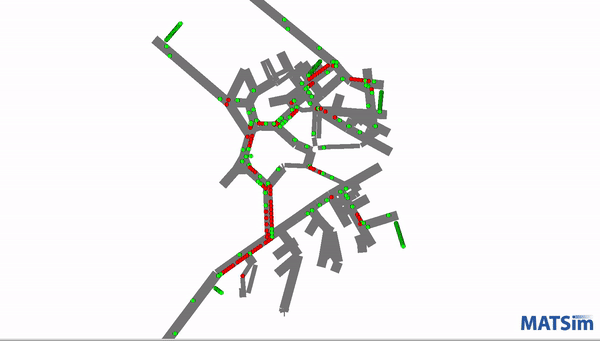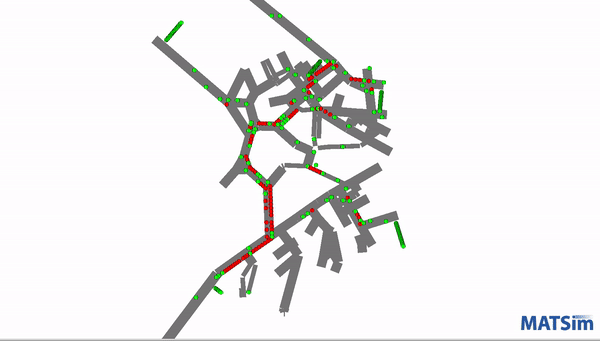
This screenshot demonstrates one of the models running as it tracks and displays movement.
Can you explain the process of evaluating different campus movements?
With each iteration, different plans are selected for each agent and assigned a score. This score is a rating of a plan’s efficiency and benefits to the agent given various costs such as travel time and distance. Optimizations are made throughout the iterations until the average score of agent plans stabilize, reaching a stochastic equilibrium rather than a best, unrealistic case. The mathematical function responsible for generating scores is called the Charypar-Nagel Utility Function. Scores are calculated by summing the utility of all activities within the plan plus the sum of all travel disutilities. Utility can be thought of as the relative importance or benefit of an activity while disutility represents the costs of travel and time spent on ineffectual activities.
How does the scoring process break down?
The first component of scores, plan utility, is the sum of the utility of each activity within the plan. An activity’s utility is generated based on the time spent completing the task given its specified importance along with negative penalties for waiting time, arriving late beyond a set threshold, and leaving an activity too early.
Plan disutility accounts for the second portion of a score and is the sum of the disutility of all travel among activities within a plan. Agent movement between two activities, called a trip, is composed of legs which delineate the use of different modes of transportation within a trip. For example, an agent traveling from home to work may commute part way by bike and part by bus. This trip would be composed of two legs. Travel disutility of a trip is the sum of the disutility scores for each leg. A leg’s score is its nonnegative utility, given the assigned mode of transportation, plus the negative monetary, time, and distance costs of travel. These costs grow linearly as travel distance and duration increase. Due to unavoidable costs, plan disutility is always a negative value.
How do scores change in response to potential model modifications?
Because of the decreasing returns of any activity, the rate of increase in activity scores declines over time. In other words, an activity is beneficial for the agent, but this benefit decreases the longer they remain at the location. This is particularly relevant with activities identified as extraneous or low importance by the user. Additionally, travel time and distance detracts from the benefit of activities, resulting in a lower score. Thus, to maximize scores we aim to decrease travel time, while increasing the utility or benefit of available activities. Collectively, a score is a measure of how worthwhile a plan is given the efficiency of its components, with higher scores indicating greater overall utility.
What do you hope the impact of this work will be?
Although similar models inform important decisions regarding the placement and types of changes to national infrastructure, this small-scale model can still provide actionable information for our William & Mary community. Specifically, this tool could one day be used to optimize the accessibility of campus pathways and building entrances. This could be achieved by adjusting the scoring function for those impacted. For example, activity utility could be penalized within a plan for agents having to travel farther to an accessible entrance. Activities’ disutilities could also be impacted by the pavement type of campus pathways by assigning greater cost to travel across brick or gravel surfaces than on smooth cement.
Do you plan to revisit or update this project in the future?
Although our summer research has come to a close, we hope to make improvements to our existing work in the future so that our model more closely resembles reality. As we unpacked the math behind MATSim’s scoring function, it became clear that machine learning techniques could offer ways to improve both the assignment of plan scores and the subsequent choice of plans. Namely, an unsupervised machine learning network could be used to reduce the required number of model iterations by more quickly identifying optimal agent plans. Additionally, access to larger amounts of data promotes model accuracy by improving the overall representation of a population. Our data consisted of GPS coordinates which were generated by MATSim; however, we plan to shift towards using dynamically collected data from MoveFlow.
How can MoveFlow help to enhance your model?
MoveFlow is a new application that collects real time location data from your smartphone in exchange for a cryptocurrency called FlowCoins. As users move about their day, their current latitude, longitude, and speed are recorded. These components allow us to discern the method of transportation used and provide meaningful temporal context, which in turn help inform model plans. By piping this location data directly into our program, we can produce real-time, predicted, and accurately calculated trajectories rather than relying on the hypothetical travel diaries of agents. This change will be made possible as the MoveFlow app goes public in the near future.
How did researching as a GRI Summer Fellow change your perspective?
In a broader sense, this research experience revealed information that pressed me to consider topics such as community development, equity, access, and additional ethical issues that extend beyond our campus. I truly enjoyed learning how to construct this model from the ground up and hope to continue my research while exploring applications that could benefit a broader community.
Does your research have implications beyond W&M? Can you talk about your work in a global context?
Although this model was constrained to the W&M campus due to limitations such as computer memory and spatial data access, our hope is to model developing areas globally. These models could be a pivotal tool in strategic planning efforts, saving both time and money. Previously, changes to infrastructure such as the addition of a road or bridge were geographically placed based often on live observations made by transportation officials. This process is incapable of capturing the movement of a population in its entirety, leading to costly errors that could place additional strain on a weak network. Using these models, we can optimize transportation by identifying ways to improve existing infrastructure while minimizing cost and maximizing both access and traffic flow.




No comments.
Comments are currently closed. Comments are closed on all posts older than one year, and for those in our archive.